Nicolò Vignatavan - Il rapporto incrementale in un intorno circolare ad un punto della funzione come definizione di derivata e l'orbita di un pianeta
Il rapporto incrementale in un intorno circolare ad un punto della funzione come definizione di derivata e l'orbita di un pianeta
Nicolò Vignatavan
Su Google Drive: https://drive.google.com/open?id=1S6JCgx86jT4RmRl3aEJjvAdP9Freg9UX
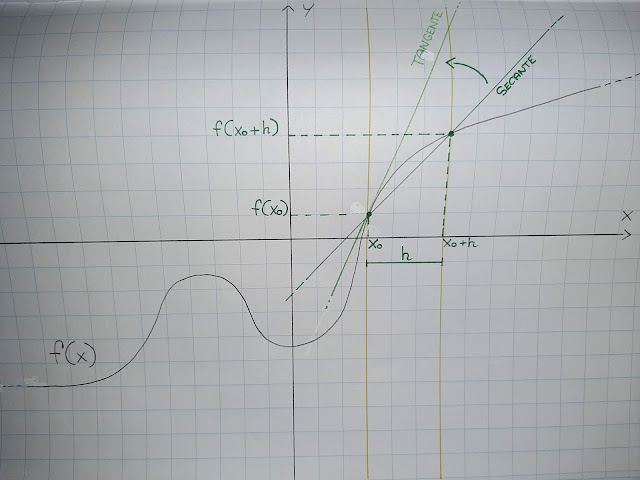
Secondo la matematica tradizionale, la derivata di una funzione in un suo punto "Xo" equivale, infinitesimamente, al rapporto incrementale [f(Xo + h) - f(Xo)] / h, con "h" inteso come "Delta x", ovvero la differenza tra l'ascissa dell'estremo superiore, in verso x, del segmento di dimensione "h", costruito a partire da "Xo" e il punto di estremo inferiore "Xo" medesimo ed "[f(Xo + h) - f(Xo)]" inteso come "Delta y", con "f(Xo + h)" ed "f(X)" considerate rispettivamente come le immagini sull'asse delle ordinate dei due punti di estremo a denominatore, con h tendente a 0.
In questi termini, ipotizzando una retta secante alla funzione precisamente nei punti di ordinata "f(Xo + h)" e "f(Xo)", considerati come le intersezioni della funzione medesima con gli estremi dell'intervallo "x" chiuso e derivabile in cui è analizzata, nell'istante in cui h tende infinitesimamente a 0, la retta diviene tangente alla funzione nel punto "Xo". Il coefficiente angolare di tale retta, nel momento di tangenza, viene definito come il valore numerico della derivata prima della funzione in tal punto.
Nel caso h si eguagliasse a 0, la retta si separerebbe dalla funzione, allontanandosi esternamente.
Ipotizziamo ,ora, lungo l'asse delle ascisse, al posto di costruire in verso "x" un segmento "h" a partire dal punto "Xo", di impostare un intorno circolare del punto "Xo", di dimensione "2h", costruendo, a partire dal punto "Xo", lungo l'asse x, un segmento "h" in direzione -oo ed un altro della stessa lunghezza in direzione +oo.
In questo modo, il rapporto incrementale risulterà [f(Xo + h) - f(Xo - h)] / 2h
Se nel primo caso, la retta secante, al tendere di h a 0, diventa tangente al punto "Xo" ruotando se stessa, poichè un estremo risulta un vincolo fisso e l'altro è mobile, nel secondo caso, presentandosi a priori un intorno circolare del punto "Xo", dunque due distanze "h" equivalenti lungo l'asse x, la retta secante diventa tangente non solo ruotando se stessa, bensì anche variando in ordinata il proprio grafico, il cui coefficiente angolare sarà, sul finire del movimento, quello della retta tangente al punto "Xo", (solo ed unico secondo il teorema di Lagrange).
A mio parere, questa seconda impostazione risulta la più completa per definire algebricamente il concetto di derivata, poichè, se nel primo caso il coefficiente angolare della retta tangente al punto "Xo" si ricava esattamente nell'infinitesimo istante finale del ciclo che impone ad "h" di tendere a 0, infinitesimamente dopo che la retta da secante diventa tangente alla funzione nel punto "Xo" ed infinitesimamente prima che la retta da tangente al punto "Xo" diventi esterna alla funzione, nel secondo caso, nella fase finale del ciclo, l'inclinazione della retta tangente si è già stabilizzata nell'ordine di grandezza di quella della futura retta tangente al punto "Xo", presi a campione statisticamente infiniti punti "Xo" lungo il grafico della funzione e, in quest'ottica, in termini di ricorrenze statistiche, nel penultimo istante prima che la retta da secante diventi tangente al punto a campione considerato, il coefficiente angolare della retta tangente si avvicinerà infinitesimamente di più a quello della retta tangente nella seconda definizione esaminata rispetto alla prima.
La definizione fisica di derivata di una funzione curvilinea al variare dell'eccentricità della circonferenza costruita su un suo arco
Sia disegnato il grafico di una funzione curvilinea a campione sul piano cartesiano xy.
Identifichiamo, sempre a campione, un punto Xo sull'asse delle ascisse ed, imposto un intorno a tale punto, consideriamo il relativo intervallo [a,b] del grafico che tale intorno intercetta sul piano cartesiano.
Studiando, dal suo lato concavo, il grafico sezionato, consideriamolo come un arco irregolare ab composto, in una visione schematizzata, da 4 coordinate: il punto Xo proiettato ortogonalmente dall'asse delle ascisse sulla curva, il punto di pancia p corrispondente al massimo/minimo della funzione nell'intervallo considerato ed i due punti di estremo a e b. La derivata prima della funzione curvilinea in Xo risulterà equivalente al coefficiente angolare della retta t passante per Xo, discorde per direzione rispetto alla crescenza/descrescenza del tratto di corda su cui giace p e perpendicolare al raggio della circonferenza costruita sull'arco concavo ab, passante per i punti a,b e Xo, nel momento in cui la sua eccentricità tenderà, in termini infinitesimi, a 0.
Negli stessi termini, volendo sviluppare un parallelismo, così come enunciato da Newton e Galileo, ipotizziamo un classico sistema geofisico nel quale attorno ad un sole, posizionato in uno dei due fuochi dell'orbita ellittica, a causa dell'attrazione gravitazionale centripeta, ruoti un suo pianeta: nell'istante in cui tale forza si annullasse, il pianeta (considerato come il nostro punto a o b), come si suol dire nel gergo comune, "partirebbe per la tangente" e dunque percorrerebbe all'infinito la direzione della tangente, identificando, su un ipotetico piano cartesiano, il suo coefficiente angolare che coinciderebbe con la derivata prima della funzione nel medesimo punto, con eccentricità tendente a 0.
Nicolò Vignatavan
Su Google Drive: https://drive.google.com/open?id=1S6JCgx86jT4RmRl3aEJjvAdP9Freg9UX
Secondo la matematica tradizionale, la derivata di una funzione in un suo punto "Xo" equivale, infinitesimamente, al rapporto incrementale [f(Xo + h) - f(Xo)] / h, con "h" inteso come "Delta x", ovvero la differenza tra l'ascissa dell'estremo superiore, in verso x, del segmento di dimensione "h", costruito a partire da "Xo" e il punto di estremo inferiore "Xo" medesimo ed "[f(Xo + h) - f(Xo)]" inteso come "Delta y", con "f(Xo + h)" ed "f(X)" considerate rispettivamente come le immagini sull'asse delle ordinate dei due punti di estremo a denominatore, con h tendente a 0.
In questi termini, ipotizzando una retta secante alla funzione precisamente nei punti di ordinata "f(Xo + h)" e "f(Xo)", considerati come le intersezioni della funzione medesima con gli estremi dell'intervallo "x" chiuso e derivabile in cui è analizzata, nell'istante in cui h tende infinitesimamente a 0, la retta diviene tangente alla funzione nel punto "Xo". Il coefficiente angolare di tale retta, nel momento di tangenza, viene definito come il valore numerico della derivata prima della funzione in tal punto.
Nel caso h si eguagliasse a 0, la retta si separerebbe dalla funzione, allontanandosi esternamente.
Ipotizziamo ,ora, lungo l'asse delle ascisse, al posto di costruire in verso "x" un segmento "h" a partire dal punto "Xo", di impostare un intorno circolare del punto "Xo", di dimensione "2h", costruendo, a partire dal punto "Xo", lungo l'asse x, un segmento "h" in direzione -oo ed un altro della stessa lunghezza in direzione +oo.
In questo modo, il rapporto incrementale risulterà [f(Xo + h) - f(Xo - h)] / 2h
Se nel primo caso, la retta secante, al tendere di h a 0, diventa tangente al punto "Xo" ruotando se stessa, poichè un estremo risulta un vincolo fisso e l'altro è mobile, nel secondo caso, presentandosi a priori un intorno circolare del punto "Xo", dunque due distanze "h" equivalenti lungo l'asse x, la retta secante diventa tangente non solo ruotando se stessa, bensì anche variando in ordinata il proprio grafico, il cui coefficiente angolare sarà, sul finire del movimento, quello della retta tangente al punto "Xo", (solo ed unico secondo il teorema di Lagrange).
A mio parere, questa seconda impostazione risulta la più completa per definire algebricamente il concetto di derivata, poichè, se nel primo caso il coefficiente angolare della retta tangente al punto "Xo" si ricava esattamente nell'infinitesimo istante finale del ciclo che impone ad "h" di tendere a 0, infinitesimamente dopo che la retta da secante diventa tangente alla funzione nel punto "Xo" ed infinitesimamente prima che la retta da tangente al punto "Xo" diventi esterna alla funzione, nel secondo caso, nella fase finale del ciclo, l'inclinazione della retta tangente si è già stabilizzata nell'ordine di grandezza di quella della futura retta tangente al punto "Xo", presi a campione statisticamente infiniti punti "Xo" lungo il grafico della funzione e, in quest'ottica, in termini di ricorrenze statistiche, nel penultimo istante prima che la retta da secante diventi tangente al punto a campione considerato, il coefficiente angolare della retta tangente si avvicinerà infinitesimamente di più a quello della retta tangente nella seconda definizione esaminata rispetto alla prima.
La definizione fisica di derivata di una funzione curvilinea al variare dell'eccentricità della circonferenza costruita su un suo arco
Sia disegnato il grafico di una funzione curvilinea a campione sul piano cartesiano xy.
Identifichiamo, sempre a campione, un punto Xo sull'asse delle ascisse ed, imposto un intorno a tale punto, consideriamo il relativo intervallo [a,b] del grafico che tale intorno intercetta sul piano cartesiano.
Studiando, dal suo lato concavo, il grafico sezionato, consideriamolo come un arco irregolare ab composto, in una visione schematizzata, da 4 coordinate: il punto Xo proiettato ortogonalmente dall'asse delle ascisse sulla curva, il punto di pancia p corrispondente al massimo/minimo della funzione nell'intervallo considerato ed i due punti di estremo a e b. La derivata prima della funzione curvilinea in Xo risulterà equivalente al coefficiente angolare della retta t passante per Xo, discorde per direzione rispetto alla crescenza/descrescenza del tratto di corda su cui giace p e perpendicolare al raggio della circonferenza costruita sull'arco concavo ab, passante per i punti a,b e Xo, nel momento in cui la sua eccentricità tenderà, in termini infinitesimi, a 0.
Negli stessi termini, volendo sviluppare un parallelismo, così come enunciato da Newton e Galileo, ipotizziamo un classico sistema geofisico nel quale attorno ad un sole, posizionato in uno dei due fuochi dell'orbita ellittica, a causa dell'attrazione gravitazionale centripeta, ruoti un suo pianeta: nell'istante in cui tale forza si annullasse, il pianeta (considerato come il nostro punto a o b), come si suol dire nel gergo comune, "partirebbe per la tangente" e dunque percorrerebbe all'infinito la direzione della tangente, identificando, su un ipotetico piano cartesiano, il suo coefficiente angolare che coinciderebbe con la derivata prima della funzione nel medesimo punto, con eccentricità tendente a 0.


Commenti
Posta un commento